いろいろ ルートにが無理数であることの証明 319480

しかし, e の定義より2 < e < 3 であるから, これは不 合理である ゆえに, eは無理数であることが証明された // 次に, 関数の値の近似値の誤差評価に関する次の定理を得る 定理512 関数f(x) は区間I においてn回微分可能であると する さらに, 正の定数M が存在Mixi数学 背理法を用いずに「ルート2は無理数である」を証明 「\sqrt{2}（ルート2）は無理数である」 背理法を用いた証明は非常に有名です． しかし，背理法を使わない証明はあまり聞いたことがありません． いろいろな証明方法が予想されますが， 2以上の整数a は無理数乗 \(n\) が円周率 \(π≒314\) やネイピア数 \(e≒2718\) 、2の平方根 \(\sqrt{2}≒1414\) といった無理数の場合は、 無理数のそばには必ず「非常に近い値の有理数」が存在する ことを利用します。 たとえば、\(2^π\) の場合。

有理数と無理数の違い 見分け方が超簡単にわかる問題を作った 中学や高校の数学の計算問題

ルートにが無理数であることの証明

ルートにが無理数であることの証明- 無理数になるんでないべか、と思う人もいるかもしれませんが 適当な有理数 a と無理数 b について (ab)(ab) = 2a となって、(2) の結果から ab と ab は無理数であることにより、無理数の和が有理数になりましたっ！ \(~\sqrt{2}~\)が無理数であることの証明の多くは、偶数奇数に注目したものが多いですが、今回は正方形の面積を使った珍しい証明方法を紹介します。 Ⅰ 命題と予備知識 Ⅱ 面積を利用した証明 Ⅰ 命題と予備知識 命題 \( \sqrt{2} \)は無理数である。

ルート2が無理数であることを背理法を使って証明せよ Yahoo 知恵袋

背理法被害者の会 新設 07月06日 脱背理法 と大学入試問題 脱背理法と大学入試問題 この頁のみ見る方のため、他の頁と重複することも書きます。 十数年前から脱背理法教育 (通常背理法で証明される定理を背理法を用いず証明する)を 東京理科大学数学 ルート2が無理数であることの証明 論理 代数 本稿では、 が 無理数 であることの証明を紹介します。 が 有理数 であると仮定すると、互いに素な整数 を用いて √2 = p q 2 = p q と表すことができます。 これより、 p2 = 2q2 p 2 = 2 q 2 となります。 つまり 無理数の例2 「平方根（ルート）」 中3数学でならった 「平方根」 も無理数だよ。ルートとよばれてるやつだ。 ルートがついているやつはたいてい無理数だね。 たとえば、良く登場してくる、 ルート2 は圧倒的に無理数だね。 なぜなら、

ルート2の無理性を、背理法を使わずに証明する 解説・講座 この動画は、日曜数学 Advent Calendar 16（http//wwwadventarorg規約分数のことですね まず無理数と証明するために有理数だと仮定しますよね？ 有理数であると言うことは必ず分数で表せれます とすると循環小数も分数で表わせれるので有理数ですね そうすると分数にできないと言うことが証明でき√3は無理数だということが証明できます なぜ互いに素な 証明「√3は無理数」 対偶による証明 命題とその対偶の真偽は一致するので、命題を直接証明するのが難しい場合、対偶を証明してもよい。 背理法 命題が成り立たないと仮定して、その矛盾を導く。 つぎの命題を証明せよ。 nを整数とするとき、n 2 が3

 ルート2が無理数であることの証明 マスマスターの思考回路 背理法を用いるときは、まず結論を否定してください。 今回は「無理数である」ことが結論になっていますが、その否定は「無理数でない」つまり「有理数である」となります。 しかし 背理法（ルート2、ルート3の証明） 背理法（無理数であることの証明） 背理法（結論が「かつ」） まとめ！ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる！ こちらの関連記事はいかがでしょうか？ 円周率πが無理数であることの証明円周率(円の周の長さと直径の比)が無理数である, つまり (整数)/(整数) と分数の形で表せないことはよく知られています\(\sqrt{2}\)や, \(\log_{10}{2}\)が無理数であることの証

中学数学 平方根 のコツ 有理数と無理数 循環小数と分数

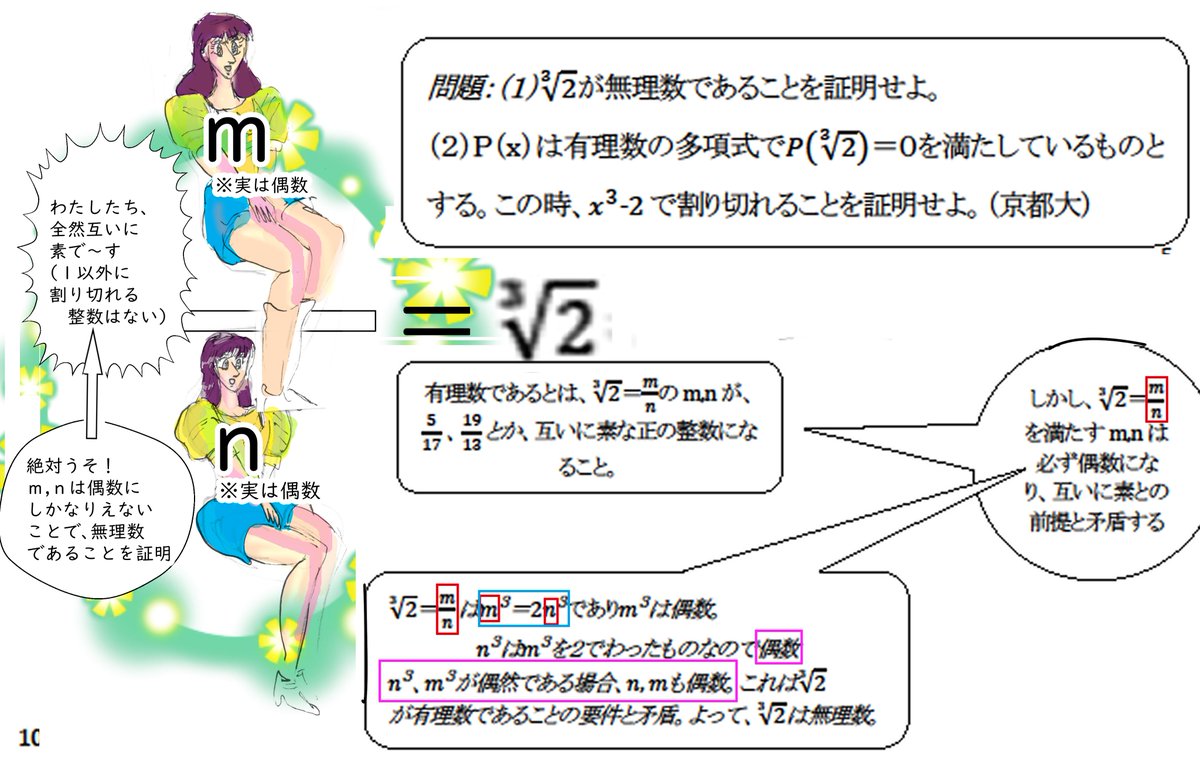
Pは無理数 の証明 怜悧玲瓏 高校数学を天空から俯瞰する

 Eが無理数であることの証明 この小論は，「eは無理数である」ことを，高校の数学を学んだ生徒に理解しやすいような形で 証明することを目的としている． 1 準備 1．1 無限級数の和について この小論に登場する無限級数は，すべて和を持つものだけであることを断っておく．π e π は、ネ 2の3乗根が無理数であることの証明（背理法） $\sqrt3{2}$ が無理数であることを示してみましょう。基本的には、 $\sqrt{2}$ が無理数であることの証明と同じ流れです（参考：基本背理法）。 大きな方針としては、「もし有理数だったら矛盾することを示す」という背理法を使った証明です。 ルート2が無理数である証明 ここまでは「2つの整数 a , b を使って a b と表せる数」である有理数を見てきました。 その反対で「2つの整数 a , b を使って a b と表すことができない数」が、無理数です。 代表的な無理数としては、 2 の正の平方根 2 ≒ 1414 が

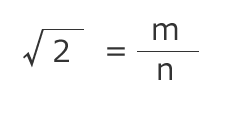
2が無理数である証明 実数 有理数 無理数 優技録

無限降下法とは フェルマーの最終定理などの応用例３選を解説 遊ぶ数学

背理法で示す。 √πが有理数であると仮定する。 √π＝n/m(m、nは互いに素な自然数)とおける。 両辺を2乗して π＝n²/m² しかし、πは無理数より、左辺は無理数であるが、右辺は有理数であるので矛盾する。 よって√πは無理数。 無理数の証明は背理法を使うことが多いです。無理数はそれ以外の数！ すごい！よく理解できているじゃん！ いま有理数の具体的な例を上げてくれたけど、無理数の例は上げられる？ 無理数の具体的な例？？？ うーん あっ！ $$\sqrt{2}$$みたいな、ルートの数って無理数だったよねー！ よく覚えてるね！ 円周率が無理数であることの証明 を行います。 この問題に取り組むにあたって、部分積分を何度も使用しますので、部分積分に慣れていない方はこちらを見て部分積分の計算に慣れましょう。 計算に慣れていないと泥沼にはまり込んでしまいます

背理法による証明 2 6が無理数である 数学i 命題と証明 5 Youtube

２が無理数であることを用いて ３ ２が無理数であることを Yahoo 知恵袋

 無理数の稠密性の証明 有理数よりも無理数の方がたくさんありそうですよね。 有理数全体が稠密集合なのだから無理数全体も稠密集合なはずです。 無理数が稠密であることの証明を3通り紹介します。 証明1 2 \sqrt {2} 2 ルート2が無理数であることの4通りの証明 高校数学の美しい物語で4つの証明が紹介されていた。 1番目はよくある偶数を使ったもの。 2番目を引用する。 が有理数 を満たす整数 が存在する なので， を満たす整数 が存在しないことを証明すればよい。P i は因数分解すると素因数の冪が総て1である数とします。 このより広い範囲でも問題4の定理が成立すれば、その一部である問題4でも成立することが証明されたことになります。 ＜記号＞ （1） 形式上 P 0 ＝1とします。

なぜ二乗して 3分の1が出てくるのか教えてください Clearnote

ルート3が無理数であることを証明せよ 世界変動展望

無理数の代表として挙げられる\\( \\sqrt{2} \\)。この\\( \\sqrt{2} \\)が無理数であることの証明を2通り紹介します。 ①命題と予備知識 ②一般的な証明 ③素因数2の偶奇を利用した証明 上の方法以外の奇抜な証明方法もあります。→「√2が無理数であることの証明（面積の利用）」 ①命題と予備知識 背理法とは？ ルート2が無理数である証明問題などの具体例をわかりやすく解説！ 排中律 こんにちは、ウチダです。 について、簡単に原理を説明した後、 「 √ 2 2 が無理数である」 ことの証明問題など、 よく出る問題 3 3 選 を順に解説していきが無理数であることを証明します 高校数学だけを前提に説明するので 話が長くなります 参考文献は杉浦光夫「解析入門I」p191 ¶ ライプニッツの公式 ‡ 積の微分法を一般化します n が自然数のときf(x);g(x) の積fg のn 階導関数は (fg) (n)= k=0 nCkf (k)g ¡k

背理法を利用してルート3が無理数であることを証明する問題で1以外に正の公約数 Clearnote

高校数学 無理数であることの証明 背理法 練習編 映像授業のtry It トライイット

面白いことが書いてあるので、色々検索されたページを参考にして 「 が無理数であることの幾何学的証明」を付け加えることにしました。 英語圏ではピタゴラス学派が 「 が無理数であること」を幾何学的に 証明したと考えている人が多く、それがポピュラーである理由のようです。 ルート2 は無理数である を証明するとき、背理法を使って矛盾を証明するとき ルート2 =b分のa(ただしabは互いに素の自然数とする) bを移行して二乗すると 2×bの二乗＝aの二乗になる ここで矛盾が生じてルート2 は無理数であることが証明されたって聞いたん問 次のことを証明せよ (1) √2 は無理数である(2) √6 は無理数である解法の丸暗記に嫌気がさしたときに見る動画。解答の背後にある考え方を

三石 数学塾 ルート２が無理数であること

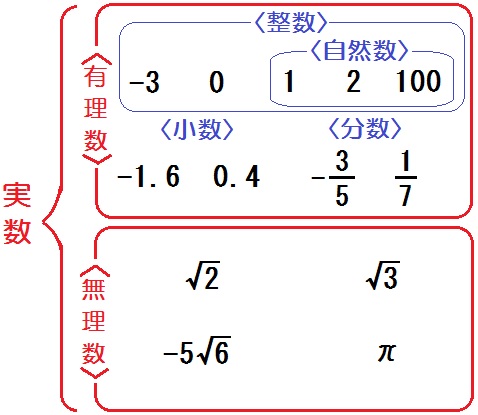
中学数学 平方根 のコツ 有理数と無理数 循環小数と分数

 ルート2が無理数であることを証明するのですが・・・教科書にはルート2が無理数でないと仮定すると、ある有理数に等しいから1以外に公約数を持たない自然数a,bを用いて、→こうする意味はなんですか？ルート2 数学 解決済 教えて！goo

6が無理数であることを用いて 次の命題を証明せよ Clearnote

背理法とは ルート2が無理数である証明問題などの具体例をわかりやすく解説 排中律 遊ぶ数学

無理数

ルート２が無理数であることの４通りの証明 高校数学の美しい物語

有理数と無理数の違い 見分け方が超簡単にわかる問題を作った 中学や高校の数学の計算問題

Pは無理数 の証明 怜悧玲瓏 高校数学を天空から俯瞰する

数学 背理法による証明の解答例まとめ 数スタ

ルート2が無理数であることの証明 数式で独楽する

背理法とは 例題を証明しながら徹底的に解説します Studyplus スタディプラス

有理数と無理数の違い ルート２が無理数であることの証明 アタリマエ

数a 2が無理数であることを証明せよ 背理法 Youtube

ルート２が無理数であることの４通りの証明 高校数学の美しい物語

発展 ルート2が無理数であることの証明 背理法を使わない方法 なかけんの数学ノート

無理数とは 知恵袋

数ia 背理法 6が無理数であることを利用して Youtube

無理数の無理数乗は無理数か Tsujimotterのノートブック

背理法を利用してルート２が無理数ならば１ ３ルート２は無理数 Yahoo 知恵袋

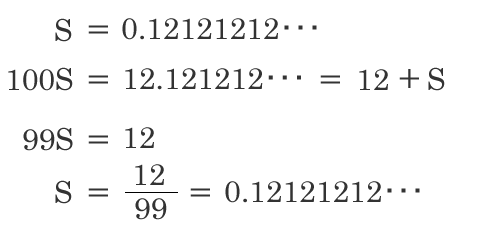
2が無理数である証明 実数 有理数 無理数 優技録

ルート2が無理数であることを背理法を使って証明せよ Yahoo 知恵袋

2の平方根 Wikipedia

無理数

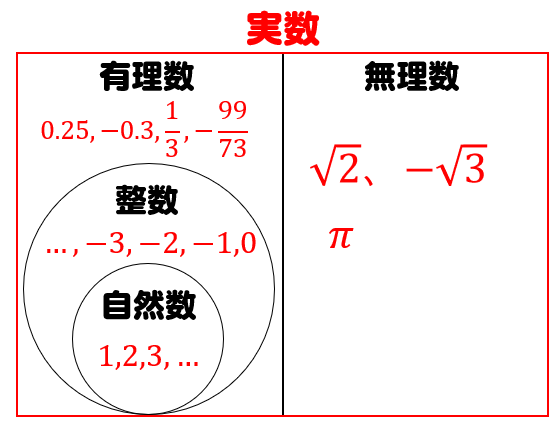
有理数 無理数とは 違いを簡単に解説 中学生が覚えるべき無理数は2種類だけ 数学fun

２０１６年 東大理系数学 第５問 具体的に調べる スケール 整数の存在証明 ガウス 背理法 オンライン受講 東大に 完全 特化 東大合格 敬天塾

無理数

有理数と無理数の違い ルート２が無理数であることの証明 アタリマエ

円周率が無理数である証明を分かりやすく説明できますか Quora

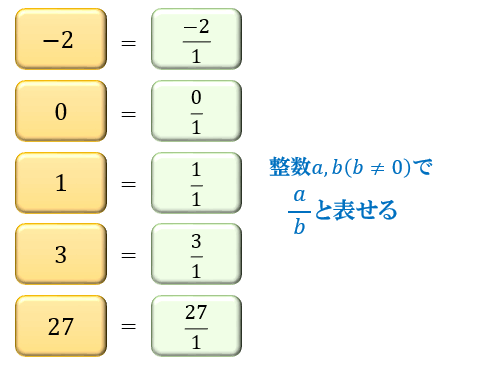
有理数と無理数の違い ルート２が無理数であることの証明 アタリマエ

3

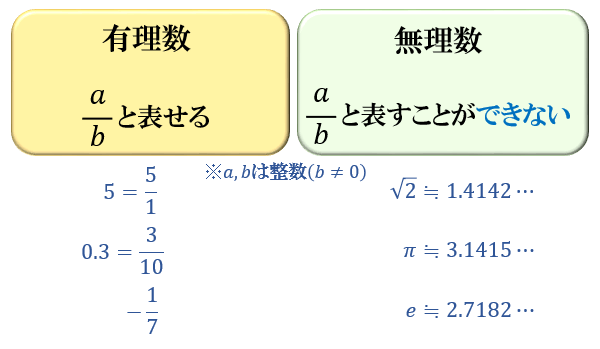
有理数と無理数の違い ルート２が無理数であることの証明 アタリマエ

高校数学 数 33 命題 続 背理法編 Youtube

背理法とは この例なら どんな馬鹿でも背理法が分かる 学生による 学生のための学問

高校数学 背理法による証明の書き方 手順 具体例を使ってわかりやすく解説 楽スタ

6が無理数であることの証明の仕方教えてください ただし Yahoo 知恵袋

ルート2が無理数であることを用いて次の命題を証明するやり方を教えてください Clear

京都大学文系 命題p あるnに対して Nと N 1 は共に有理数である 命題q すべてのnに対して N 1 Nは無理数である 受験数学かずスクール

無理数の無理数乗 有理数となる場合 年 横浜市立大 1986年 阪大 数学日和

12年京大入試理系数学第4問 ほのぼの数学がんばろう

3が無理数であることを既知として 3 5が無理数であることを証明せ 数学 教えて Goo

もたこ博士の算数工房 算数から数学まで

有理数とは 無理数とは 定義を明らかにして が無理数と証明する 数学ia Himokuri

観客 召集する ひばり 3は無理数 照明 Lunch To Sweets Jp

11 有理数 無理数の問題 京極一樹の数学塾

無理数はなぜ存在するのですか Quora

無理数の証明 1 2 3が無理数である 数学i 命題と証明 6 Youtube

例題58の解説でr 7を二乗する時に R 7 で計算するのはなぜですか Clearnote

無理数であることの証明 数学の偏差値を上げて合格を目指す

背理法とは 無理数の問題例と証明を徹底解説 理系ラボ

7が無理数であることの証明 下の画像 青チャートより Yahoo 知恵袋

無理数の発見の歴史

無理数とお友達になろう 第384回科学勉強会

5が無理数であることを 背理法を用いて証明せよ 5が無理数 Yahoo 知恵袋

結城浩 そういえば 数学ガール フェルマーの最終定理 には背理法の章があって どういう問題にしていたかというと 無理数で あることの証明 ではなく 有理数ではないことの証明 にしていました

背理法とは 例題を証明しながら徹底的に解説します Studyplus スタディプラス

11 有理数 無理数の問題 京極一樹の数学塾

2が無理数であることを証明 2を有理数と仮定した時なぜ1以外の公約 数学 教えて Goo

三石 数学塾 ルート２が無理数であること

3が無理数であることを用いて 1 3が無理数であることを証明せよ あとこ Yahoo 知恵袋

三石 数学塾 ルート２が無理数であること その２

三石 数学塾 ルート２が無理数であること その２

高校数学 無理数であることの証明 背理法 練習編 映像授業のtry It トライイット

ルート２が無理数であることの４通りの証明 高校数学の美しい物語

有理数とは 無理数とは 定義を明らかにして が無理数と証明する 数学ia Himokuri

ルート2が無理数の証明 ルート4が無理数の証明 後編

3分で分かる 有理数と無理数の違いと見分け方 練習問題付き 合格サプリ

背理法とは 無理数の問題例と証明を徹底解説 理系ラボ

ルート２が無理数であることの４通りの証明 高校数学の美しい物語

有理数と無理数の違い ルート２が無理数であることの証明 アタリマエ

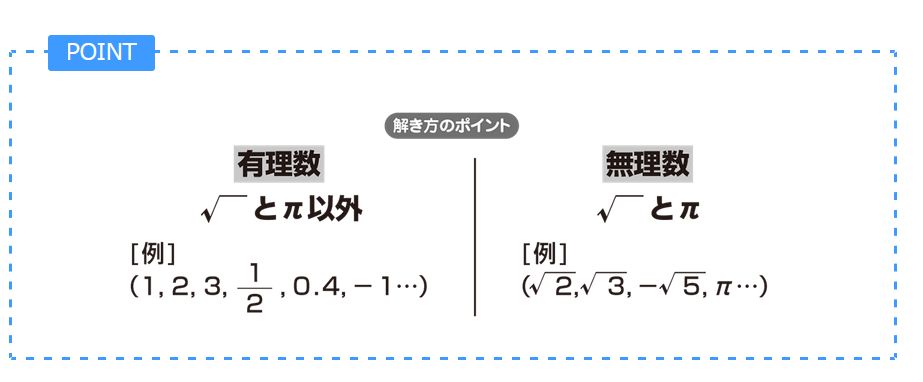
有理数と分数 無理数の違い よくある誤解を越えて 趣味の大学数学

ルート33

2が無理数であることの2つの証明 Youtube

背理法

命題 背理法を用いたルート2が無理数であることの証明 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開

3

高校数学 背理法 無理数であることの証明 有理数と無理数の等式 A B K 0 受験の月

背理法 を使いこなして証明を書こう ルート２が無理数であることの証明 についても解説 ますますmathが好きになる 魔法の数学ノート

Sin1 Cos1 は無理数か 世界変動展望

無理数とは

有理数と分数 無理数の違い よくある誤解を越えて 趣味の大学数学

無理数 Wikipedia

2が無理数であることの図形的な証明 理系のための備忘録

12年京大入試理系数学第4問 ほのぼの数学がんばろう

阪大入試問題 円周率が無理数であることを証明する

ルート5は無理数であることを証明せよ Clearnote

11 有理数 無理数の問題 京極一樹の数学塾

無理数を求める

無理数

2が無理数であることを用いて 2 2は無理数であることを証明 Yahoo 知恵袋

無理数とお友達になろう 第384回科学勉強会

2が無理数であることの図形的な証明 理系のための備忘録

高校数学 無理数であることの証明 背理法 練習編 映像授業のtry It トライイット

背理法とは ルート2が無理数である証明問題などの具体例をわかりやすく解説 排中律 遊ぶ数学

無理数の無理数乗 有理数となる場合 年 横浜市立大 1986年 阪大 数学日和